【DDIM精读】公式推导加代码分析。
【DDIM精读】公式推导加代码分析。
- 1.前言:
- ddim总览
- 2.均值(μ\muμ)
- 3.方差(σ\sigmaσ)
- 4.证明部分
- 一、论文中公式(13)的推导:
- 二、在作者给定的公式中只说明 T 时刻满足与DDPM同样的q(XT∣X0)q(X_T|X_0)q(XT∣X0), 但不能说明所有的 t 时刻,接下来就要证明:
- 5.respacing
- 6.代码分析:
- 一 、采样
- 二、respacing
- 7.Reference:
1.前言:
论文地址:https://arxiv.org/abs/2010.02502ICLR 2021
项目地址:https://github.com/openai/improved-diffusion
不啰嗦,就简单介绍采样过程的均值与方差的推导。
训练过程与DDPM差不多。
证明部分放在最后。
请注意,DDIM 论文中的 αt\alpha_tαt 是指来自 DDPM 的 αˉt{\color{lightgreen}\bar\alpha_t}αˉt。
其中 ϵτi\epsilon_{\tau_i}ϵτi 是随机噪声,τ\tauτ 是 [1,2,…,T][1,2,\dots,T][1,2,…,T] 的子序列,长度为 SSS,
DDPM的均值方差及公式推导看这篇:https://blog.csdn.net/qq_45934285/article/details/129107994?spm=1001.2014.3001.5501(DDPM是前置知识需要先看)
ddim总览
- 不同于 DDPM 基于马尔可夫的 Forward Process,DDIM 提出了 NON-MARKOVIAN FForward Processes。
- 基于这一假设,DDIM 推导出了相比于 DDPM 更快的采样过程。
- 相比于 DDPM,DDIM 的采样是确定的,即给定了同样的初始噪声xtx_txt ,DDIM 能够生成相同的结果x0x_0x0 。
- DDIM和DDPM的训练方法相同,因此在 DDPM 基础上加上 DDIM 采样方案即可。
2.均值(μ\muμ)
xτi−1=ατi−1(xτi−1−ατiϵθ(xτi)ατi)+1−ατi−1−στi2⋅ϵθ(xτi)+στiϵτix_{\tau_{i-1}} = \sqrt{\alpha_{\tau_{i-1}}}\Bigg( \frac{x_{\tau_i} - \sqrt{1 - \alpha_{\tau_i}}\epsilon_\theta(x_{\tau_i})}{\sqrt{\alpha_{\tau_i}}} \Bigg) \\ + \sqrt{1 - \alpha_{\tau_{i- 1}} - \sigma_{\tau_i}^2} \cdot \epsilon_\theta(x_{\tau_i}) \\ + \sigma_{\tau_i} \epsilon_{\tau_i} xτi−1=ατi−1(ατixτi−1−ατiϵθ(xτi))+1−ατi−1−στi2⋅ϵθ(xτi)+στiϵτi




主公式是公式(7),然后由公式(10)(9)得到最终的均值表达式

其中predicted x0部分就是将DDPM的x0的由xt和噪声的表达。
direction pointing to xt部分也是将上一步的x0代入公式(7)得到的结果。
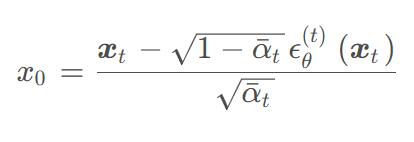
损失函数:

3.方差(σ\sigmaσ)
στi=η1−ατi−11−ατi1−ατiατi−1\sigma_{\tau_i} = \eta \sqrt{\frac{1 - \alpha_{\tau_{i-1}}}{1 - \alpha_{\tau_i}}} \sqrt{1 - \frac{\alpha_{\tau_i}}{\alpha_{\tau_{i-1}}}}στi=η1−ατi1−ατi−11−ατi−1ατi

这里考虑两种特殊情况:
如果η=0\eta = 0η=0,那么生成过程就是确定的,这种情况下为 DDIM。
如果η=1\eta = 1η=1,该前向过程变成了马尔科夫链,该生成过程等价于 DDPM 的生成过程。也就是说==当η=1\eta = 1η=1的时候,采样公式(均值)变为DDPM的采样公式。即:

将η=1\eta = 1η=1的方差公式代入到上面的均值公式中能够得到(DDPM采样公式):

证明先看:

证明:

得到上面这个结论然后代入均值公式:

4.证明部分
一、论文中公式(13)的推导:

而后进行换元,令σ=(1−αˉ/αˉ)\sigma=(\sqrt{1-\bar\alpha}/\sqrt{\bar\alpha})σ=(1−αˉ/αˉ), xˉ=x/αˉ\bar x = x/\sqrt{\bar\alpha}xˉ=x/αˉ ,带入得到:

于是,基于这个 ODE 结果,能通过xˉ(t)+dxˉ(t)\bar x({t}) + d\bar x(t)xˉ(t)+dxˉ(t)计算得到xˉ(t+1)\bar x(t+1)xˉ(t+1)与xt+1x_{t+1}xt+1
二、在作者给定的公式中只说明 T 时刻满足与DDPM同样的q(XT∣X0)q(X_T|X_0)q(XT∣X0), 但不能说明所有的 t 时刻,接下来就要证明:
前置知识:

回顾一下数学归纳法:
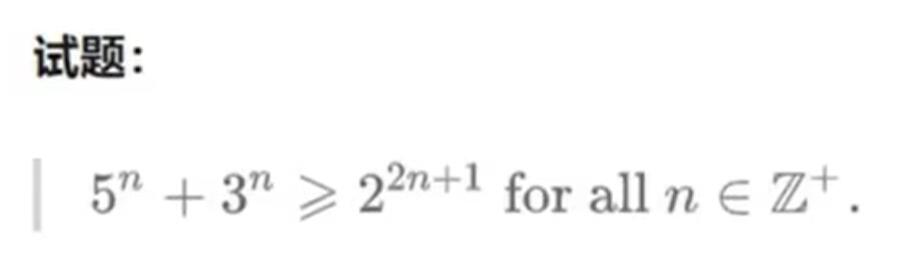

此时我们知道T时刻满足条件,首先假设t时刻也满足条件,那么如果t-1时刻也满足条件,即命题得证!


5.respacing
respacing是一种加速采样的技巧。
训练可以是一个长序列,而采样可以只在子序列上进行。

效果:

对于这个σˉ\bar \sigmaσˉ见:

6.代码分析:
代码来自文章开头的项目地址IDDPM。
一 、采样
采样函数:
def ddim_sample(self,model,x,t,clip_denoised=True,denoised_fn=None,model_kwargs=None,eta=0.0,):"""Sample x_{t-1} from the model using DDIM.Same usage as p_sample()."""out = self.p_mean_variance(model,x,t,clip_denoised=clip_denoised,denoised_fn=denoised_fn,model_kwargs=model_kwargs,)# Usually our model outputs epsilon, but we re-derive it# in case we used x_start or x_prev prediction.eps = self._predict_eps_from_xstart(x, t, out["pred_xstart"])alpha_bar = _extract_into_tensor(self.alphas_cumprod, t, x.shape)alpha_bar_prev = _extract_into_tensor(self.alphas_cumprod_prev, t, x.shape)sigma = (eta* th.sqrt((1 - alpha_bar_prev) / (1 - alpha_bar))* th.sqrt(1 - alpha_bar / alpha_bar_prev))# Equation 12.noise = th.randn_like(x)mean_pred = (out["pred_xstart"] * th.sqrt(alpha_bar_prev)+ th.sqrt(1 - alpha_bar_prev - sigma ** 2) * eps)nonzero_mask = ((t != 0).float().view(-1, *([1] * (len(x.shape) - 1)))) # no noise when t == 0sample = mean_pred + nonzero_mask * sigma * noisereturn {"sample": sample, "pred_xstart": out["pred_xstart"]}反向过程:
def ddim_reverse_sample(self,model,x,t,clip_denoised=True,denoised_fn=None,model_kwargs=None,eta=0.0,):"""Sample x_{t+1} from the model using DDIM reverse ODE."""assert eta == 0.0, "Reverse ODE only for deterministic path"out = self.p_mean_variance(model,x,t,clip_denoised=clip_denoised,denoised_fn=denoised_fn,model_kwargs=model_kwargs,)# Usually our model outputs epsilon, but we re-derive it# in case we used x_start or x_prev prediction.eps = (_extract_into_tensor(self.sqrt_recip_alphas_cumprod, t, x.shape) * x- out["pred_xstart"]) / _extract_into_tensor(self.sqrt_recipm1_alphas_cumprod, t, x.shape)alpha_bar_next = _extract_into_tensor(self.alphas_cumprod_next, t, x.shape)# Equation 12. reversedmean_pred = (out["pred_xstart"] * th.sqrt(alpha_bar_next)+ th.sqrt(1 - alpha_bar_next) * eps)return {"sample": mean_pred, "pred_xstart": out["pred_xstart"]}
循环采样:
def ddim_sample_loop(self,model,shape,noise=None,clip_denoised=True,denoised_fn=None,model_kwargs=None,device=None,progress=False,eta=0.0,):"""Generate samples from the model using DDIM.Same usage as p_sample_loop()."""final = Nonefor sample in self.ddim_sample_loop_progressive(model,shape,noise=noise,clip_denoised=clip_denoised,denoised_fn=denoised_fn,model_kwargs=model_kwargs,device=device,progress=progress,eta=eta,):final = samplereturn final["sample"]
采样主体:
def ddim_sample_loop_progressive(self,model,shape,noise=None,clip_denoised=True,denoised_fn=None,model_kwargs=None,device=None,progress=False,eta=0.0,):"""Use DDIM to sample from the model and yield intermediate samples fromeach timestep of DDIM.Same usage as p_sample_loop_progressive()."""if device is None:device = next(model.parameters()).deviceassert isinstance(shape, (tuple, list))if noise is not None:img = noiseelse:img = th.randn(*shape, device=device)indices = list(range(self.num_timesteps))[::-1]if progress:# Lazy import so that we don't depend on tqdm.from tqdm.auto import tqdmindices = tqdm(indices)for i in indices:t = th.tensor([i] * shape[0], device=device)with th.no_grad():out = self.ddim_sample(model,img,t,clip_denoised=clip_denoised,denoised_fn=denoised_fn,model_kwargs=model_kwargs,eta=eta,)yield outimg = out["sample"]
二、respacing
整个代码:代码中有注释!!!
import numpy as np
import torch as thfrom .gaussian_diffusion import GaussianDiffusiondef space_timesteps(num_timesteps, section_counts):"""Create a list of timesteps to use from an original diffusion process,given the number of timesteps we want to take from equally-sized portionsof the original process.For example, if there's 300 timesteps and the section counts are [10,15,20]then the first 100 timesteps are strided to be 10 timesteps, the second 100are strided to be 15 timesteps, and the final 100 are strided to be 20.If the stride is a string starting with "ddim", then the fixed stridingfrom the DDIM paper is used, and only one section is allowed.:param num_timesteps: the number of diffusion steps in the originalprocess to divide up.:param section_counts: either a list of numbers, or a string containingcomma-separated numbers, indicating the step countper section. As a special case, use "ddimN" where Nis a number of steps to use the striding from theDDIM paper.:return: a set of diffusion steps from the original process to use."""if isinstance(section_counts, str):if section_counts.startswith("ddim"):desired_count = int(section_counts[len("ddim") :])for i in range(1, num_timesteps):if len(range(0, num_timesteps, i)) == desired_count:return set(range(0, num_timesteps, i))raise ValueError(f"cannot create exactly {num_timesteps} steps with an integer stride")section_counts = [int(x) for x in section_counts.split(",")]size_per = num_timesteps // len(section_counts)extra = num_timesteps % len(section_counts)start_idx = 0all_steps = []for i, section_count in enumerate(section_counts):size = size_per + (1 if i < extra else 0)if size < section_count:raise ValueError(f"cannot divide section of {size} steps into {section_count}")if section_count <= 1:frac_stride = 1else:frac_stride = (size - 1) / (section_count - 1)cur_idx = 0.0taken_steps = []for _ in range(section_count):taken_steps.append(start_idx + round(cur_idx))cur_idx += frac_strideall_steps += taken_stepsstart_idx += sizereturn set(all_steps)class SpacedDiffusion(GaussianDiffusion):"""A diffusion process which can skip steps in a base diffusion process.:param use_timesteps: a collection (sequence or set) of timesteps from theoriginal diffusion process to retain.:param kwargs: the kwargs to create the base diffusion process."""def __init__(self, use_timesteps, **kwargs):self.use_timesteps = set(use_timesteps)# 指可以用的时间步,可能是步长为1,也有可能步长大于1(respacing)self.timestep_map = []# 基本等同于use_timesteps,不过是列表self.original_num_steps = len(kwargs["betas"])base_diffusion = GaussianDiffusion(**kwargs) # pylint: disable=missing-kwoa# 计算全新采样时刻后的betaslast_alpha_cumprod = 1.0# 重新定义betas序列new_betas = []for i, alpha_cumprod in enumerate(base_diffusion.alphas_cumprod):if i in self.use_timesteps:# 来自beta与alpha之间的关系式new_betas.append(1 - alpha_cumprod / last_alpha_cumprod)last_alpha_cumprod = alpha_cumprodself.timestep_map.append(i)# 更新self.betas成员变量kwargs["betas"] = np.array(new_betas)# 此处更新了betassuper().__init__(**kwargs)def p_mean_variance(self, model, *args, **kwargs): # pylint: disable=signature-differsreturn super().p_mean_variance(self._wrap_model(model), *args, **kwargs)def training_losses(self, model, *args, **kwargs): # pylint: disable=signature-differsreturn super().training_losses(self._wrap_model(model), *args, **kwargs)def _wrap_model(self, model):if isinstance(model, _WrappedModel):return modelreturn _WrappedModel(model, self.timestep_map, self.rescale_timesteps, self.original_num_steps)def _scale_timesteps(self, t):# Scaling is done by the wrapped model.return tclass _WrappedModel:def __init__(self, model, timestep_map, rescale_timesteps, original_num_steps):self.model = modelself.timestep_map = timestep_mapself.rescale_timesteps = rescale_timestepsself.original_num_steps = original_num_stepsdef __call__(self, x, ts, **kwargs):# ts是连续的索引,map_tensor中包含的是spacing后的索引# __call__的作用是将ts映射到真正的spacing后的时间步骤map_tensor = th.tensor(self.timestep_map, device=ts.device, dtype=ts.dtype)new_ts = map_tensor[ts]if self.rescale_timesteps:# 始终控制new_ts在[0,1000]以内的浮点数new_ts = new_ts.float() * (1000.0 / self.original_num_steps)return self.model(x, new_ts, **kwargs)7.Reference:
1.https://blog.csdn.net/m0_63642362/article/details/128593528?ops_request_misc=&request_id=&biz_id=102&utm_term=ddim&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduweb~default-1-128593528.142v75insert_down38,201v4add_ask,239v2insert_chatgpt&spm=1018.2226.3001.4187
2.https://www.bilibili.com/video/BV1JY4y1N7dn/?spm_id_from=333.999.0.0&vd_source=5413f4289a5882463411525768a1ee27
3.https://blog.csdn.net/weixin_43850253/article/details/128413786?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522167945157616800222855326%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=167945157616800222855326&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2alltop_click~default-2-128413786-null-null.142v75insert_down38,201v4add_ask,239v2insert_chatgpt&utm_term=ddim&spm=1018.2226.3001.4187
