【数学】基本代数图论 Basic Algebraic Graph Theory
文章目录
- 【数学】基本代数图论 Basic Algebraic Graph Theory
- 1. Notations
- 2. Basic Concepts
- 2.1 Basic Representation of Graph
- 2.2 Basic Relations of Graph
- 2.3 Subgraph of Graph
- 2.4 Adjacency Matrix
- 2.5 Laplacian Matrix
- Reference
【数学】基本代数图论 Basic Algebraic Graph Theory
1. Notations
- G\mathscr{G}G:图
- V\mathscr{V}V:节点的集合
- E\mathscr{E}E:边的集合
- A\mathscr{A}A:邻接矩阵
- L\mathscr{L}L:拉普拉斯矩阵
- Ni\mathscr{N}_iNi:智能体iii的邻居节点集合
2. Basic Concepts
2.1 Basic Representation of Graph
- 有向图 dircted graph:G≜(V,E)\mathscr{G}\triangleq(\mathscr{V,E})G≜(V,E),其中V≜{1,…,p}\mathscr{V}\triangleq{\{1,\dots,p\}}V≜{1,…,p}表示节点的集合,E⊆(V×V)\mathscr{E}\subseteq(\mathscr{V}\times{\mathscr{V}})E⊆(V×V)表示边的集合。
- 有向图的边 edge:(i,j)(i,j)(i,j)表示jjj可以从iii获取信息,但反过来则不行,且有(i,j)∈E(i,j)\in\mathscr{E}(i,j)∈E,其中iii是父节点jjj是子节点。
- 无向图的边 edge:(i,j)(i,j)(i,j)表示iii和jjj可以交换信息,无向图的边可以视作是一种特殊的有向图的边,比如无向图的边(i,j)(i,j)(i,j)可以视作有向图的边(i,j)(i,j)(i,j)和(j,i)(j,i)(j,i)的组合。
- 有权图 weighted graph:图中的每一条边都具有权重,如果没有特殊说明,基本所有的图都是有权图。
- 图集合的并 union of a collection of graphs:图集合的并是指,图的节点集合的并和图的边集合的并。
- 邻居节点集合Ni\mathscr{N}_iNi:代表了所有与智能体iii具有一条边相连的所有其他智能体构成的集合。
2.2 Basic Relations of Graph
- 有向通路 directed path:是针对有向图而言的,可以用一系列的边来表示(i1,i2),(i2,i3)(i_1,i_2),(i_2,i_3)(i1,i2),(i2,i3)
- 无向通路 undirected path:是针对无向图而言的,用类似于有向通路的方式来定义。
- 强连接 strongly connected:是针对有向图而言的,∀\forall∀节点间都∃\exists∃一条有向通路
- 连接 connected:是针对无向图而言的,∀\forall∀互异节点间都∃\exists∃一条无向通路
- 完全 complete:是针对有向图而言的,∀\forall∀节点间都∃\exists∃一条边
- 全连接 fully connected:是针对无向图而言的,∀\forall∀互异节点间都∃\exists∃一条边
- 有向树 directed tree:是针对于有向图而言的,除了根节点外每个节点都只有一个父节点,而根节点则没有父节点
- 树 tree:是针对于无向图而言的,每一对节点都只由一条无向通路连接。
2.3 Subgraph of Graph
- 子图 subgraph:(Vs,Es)(\mathscr{V}^s,\mathscr{E}^s)(Vs,Es)是(V,E)(\mathscr{V},\mathscr{E})(V,E)的子图,其中Vs⊆V,Es⊆E⋂(Vs,Vs)\mathscr{V}^s\subseteq\mathscr{V},\mathscr{E}^s\subseteq\mathscr{E}\bigcap(\mathscr{V}^s,\mathscr{V}^s)Vs⊆V,Es⊆E⋂(Vs,Vs)
- 有向生成树 directed spanning tree:(Vs,Es)(\mathscr{V}^s,\mathscr{E}^s)(Vs,Es)是(V,E)(\mathscr{V},\mathscr{E})(V,E)的子图,s.t.s.t.s.t.(Vs,Es)(\mathscr{V}^s,\mathscr{E}^s)(Vs,Es)是有向树,并且Vs=V\mathscr{V}^s=\mathscr{V}Vs=V,即子图包含原图的所有节点
- 无向生成树 undirected spanning tree:(Vs,Es)(\mathscr{V}^s,\mathscr{E}^s)(Vs,Es)是(V,E)(\mathscr{V},\mathscr{E})(V,E)的子图,s.t.s.t.s.t.(Vs,Es)(\mathscr{V}^s,\mathscr{E}^s)(Vs,Es)是树,并且Vs=V\mathscr{V}^s=\mathscr{V}Vs=V,即子图包含原图的所有节点
- 有向生成树的存在性 existence of directed spanning tree:当有向生成树是图(V,E)(\mathscr{V},\mathscr{E})(V,E)的子图的时候,我们称图(V,E)(\mathscr{V},\mathscr{E})(V,E)具有生成树。判据:图(V,E)(\mathscr{V},\mathscr{E})(V,E)具有生成树iffiffiff图(V,E)(\mathscr{V},\mathscr{E})(V,E)至少具有一个节点对其他所有的节点具有有向通路。
- 无向图生成树的存在性 existence of undirected spanning tree:无向图生成树的存在性等同于连接性。
2.4 Adjacency Matrix
- 有向图的邻接矩阵 adjacency matrix of direceted graph:不允许有自边self-edge的图(V,E)(\mathscr{V},\mathscr{E})(V,E)的邻接矩阵可以表示为A≜[aij]∈Rp×p\mathscr{A}\triangleq[a_{ij}]\in\mathbb{R}^{p\times{p}}A≜[aij]∈Rp×p,
aij={positive weightif(j,i)∈E0if(j,i)∉E0ifi=ja_{ij}= \left\{\begin{array}{ll} \begin{aligned} & \textrm{positive weight} & \textrm{if$(j,i)\in\mathscr{E}$} \\ & 0 & \textrm{if$(j,i)\notin\mathscr{E}$} \\ & 0 & \textrm{if$i=j$} \end{aligned} \end{array}\right. aij=⎩⎨⎧positive weight00if(j,i)∈Eif(j,i)∈/Eifi=j
- 无向图的邻接矩阵 adjacency matrix of undirected graph:无向图的邻接矩阵定义类似,只不过多了一条性质是aij=aji,i≠ja_{ij}=a_{ji},i\neq{j}aij=aji,i=j,保证了无向图的邻接矩阵是对称的。
- 节点的入度 in-degree:对节点iii来说,其入度是∑j=1paij\sum_{j=1}^{p}a_{ij}∑j=1paij
- 节点的出度out-degree:对节点iii来说,其出度是∑j=1paji\sum_{j=1}^{p}a_{ji}∑j=1paji
- 平衡点 balanced node:对于节点iii来说,如果它的入度等于出度,那么它是平衡点。
- 平衡图 balanced graph:对于图来说,如果它的所有结点都是平衡点那么该图则是平衡图。
2.5 Laplacian Matrix
拉普拉斯矩阵 Laplacian Matrix的定义是L≜[ℓij]∈Rp×p\mathscr{L}\triangleq[\ell_{ij}]\in\mathbb{R}^{p\times{p}}L≜[ℓij]∈Rp×p
ℓii=∑j=1,i≠jpaij,ℓij=−aij,i≠j\ell_{ii}=\sum_{j=1,i\ne{j}}^{p}a_{ij}, \quad \ell_{ij}=-a_{ij},i\ne{j} ℓii=j=1,i=j∑paij,ℓij=−aij,i=j
并且注意到(j,i)∉E(j,i)\notin\mathscr{E}(j,i)∈/E则有ℓij=−aij=0\ell_{ij}=-a_{ij}=0ℓij=−aij=0,那么拉普拉斯矩阵满足:
ℓij≤0,i≠j,∑j=1pℓij=0,i=1,…,p\ell_{ij}\le0,i\ne{j}, \quad \sum_{j=1}^p\ell_{ij}=0,i=1,\dots,p ℓij≤0,i=j,j=1∑pℓij=0,i=1,…,p
- 无向图的拉普拉斯矩阵是对称阵,直接称为Laplacian matrix
- 有向图的拉普拉斯矩阵是非对称阵,称为nonsymetric Laplacian matrix或者directed Laplacian matrix
入度矩阵in-degree matrix D≜[dij]∈Rp×pD\triangleq[d_{ij}]\in\mathbb{R}^{p\times{p}}D≜[dij]∈Rp×p的定义是:
dij={0if i≠j∑j=1paiji=1,…,pd_{ij}= \left\{\begin{array}{ll} \begin{aligned} & 0 & \textrm{if $i\ne{j}$} \\ & \sum_{j=1}^pa_{ij} & i=1,\dots,p \end{aligned} \end{array}\right. dij=⎩⎨⎧0j=1∑paijif i=ji=1,…,p
那么拉普拉斯矩阵L\mathscr{L}L就可以通过入度矩阵DDD和邻接矩阵A\mathscr{A}A来进行表示
L=D−A\mathscr{L}=D-\mathscr{A} L=D−A
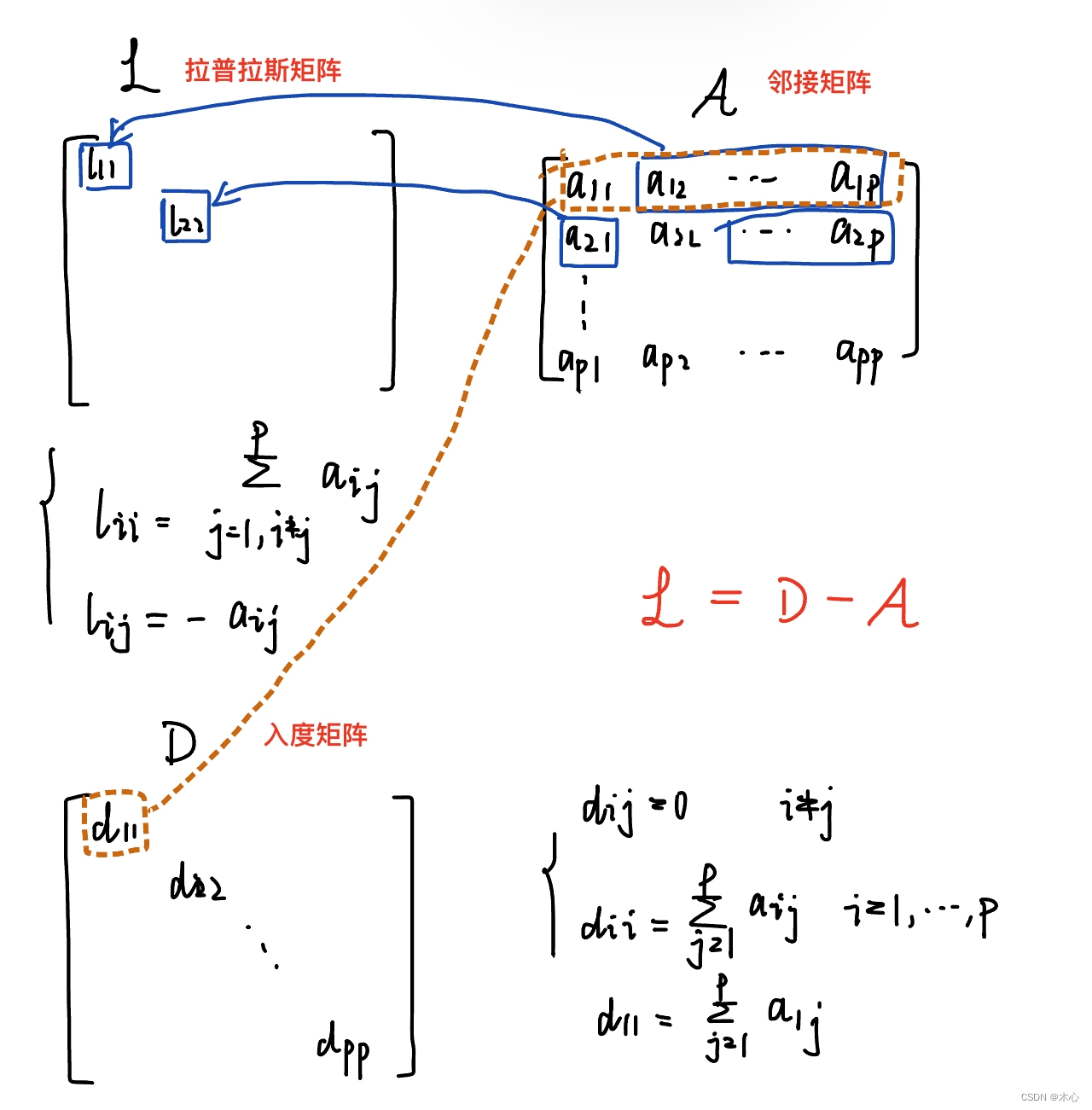
三者基本的关系可以由上图表示。
Reference
Distributed Coordination of Multi-agent Networks Emergent Problems, Models, and Issues
