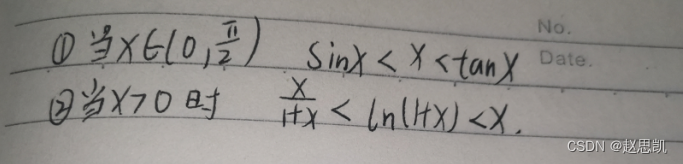微分中值定理
创始人
2025-05-31 03:18:25
极值
目录
极值
费马引理
编辑
罗尔定理
拉格朗日中值定理
例题:
例2
例3
两个重要结论:
编辑
柯西中值定理:

如何用自己的语言理解极值呢?

极大值和极小值的类似,我们不再进行说明
极值点有什么特点吗?
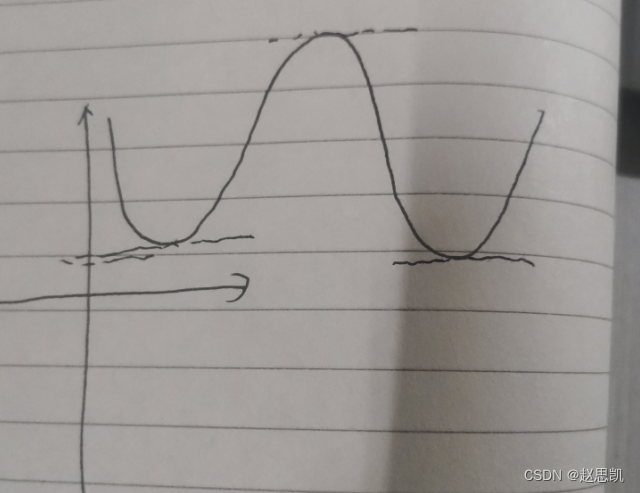
我们发现,极值点的斜率为0,并且切线平行与x轴,导数为0.
费马引理
简单的说极值点可导的话,导数为0
我们对费马引理进行证明:

罗尔定理

如果函数在闭区间[a,b]连续,开区间(a,b)可导,并且端点值f(a)=f(b),那么在该区间存在一定,使这一点的导数为0.
我们随便画出一个图像:
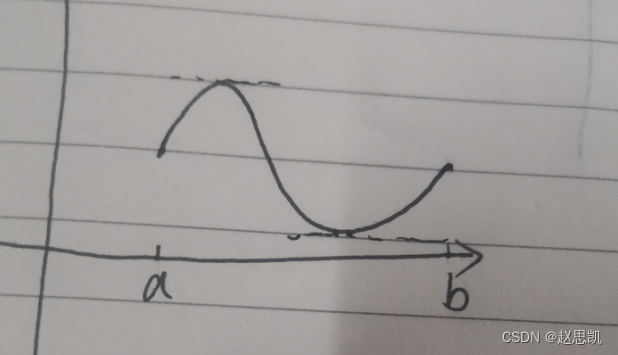
我们进行证明

罗尔定理的几何意义
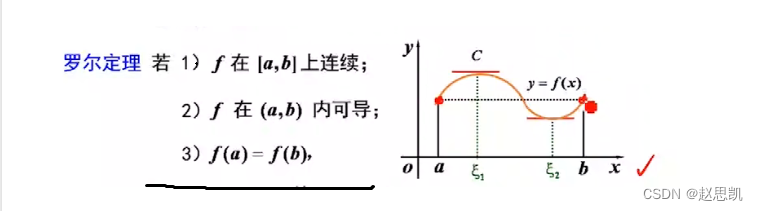
我们可以发现,存在的点柯西与其说是平行于x轴不如说是平行于连接a,b两个端点的直线。
由此,我们引入拉格朗日中值定理
拉格朗日中值定理
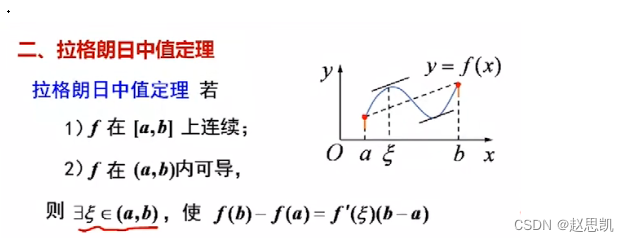

我们可以把式子进行改写:
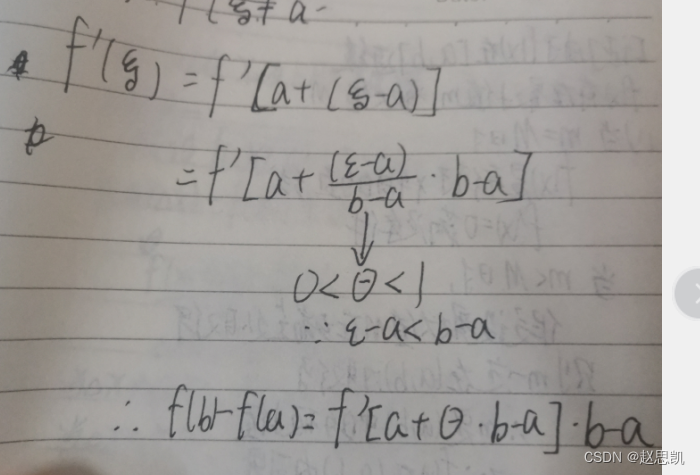
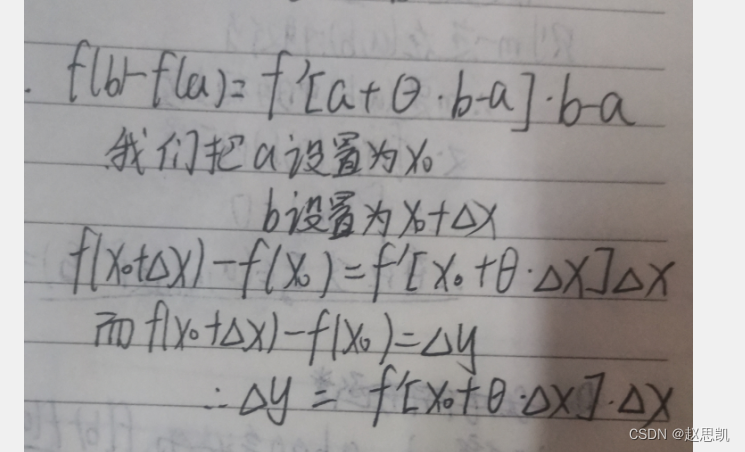
而在微分中,我们又了解到函数改变量等于自变量的改变量×这一点的改变量
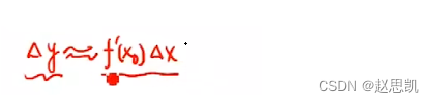
这就是函数增量的大概表示。
而这一个是函数增量的具体表示
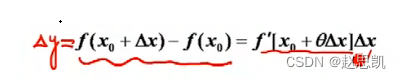

我们进行证明:

例题:
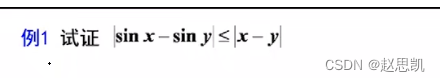
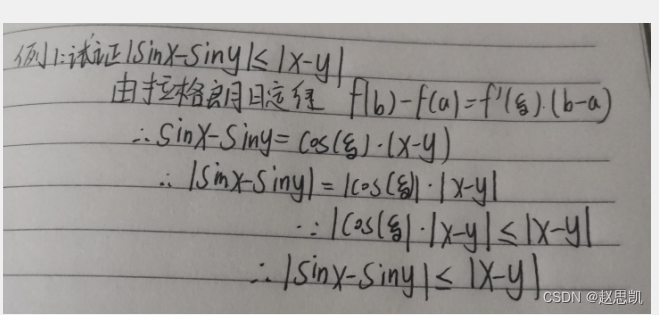
例2
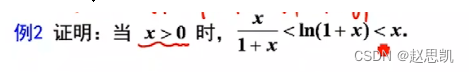

例3


两个重要结论:
柯西中值定理:
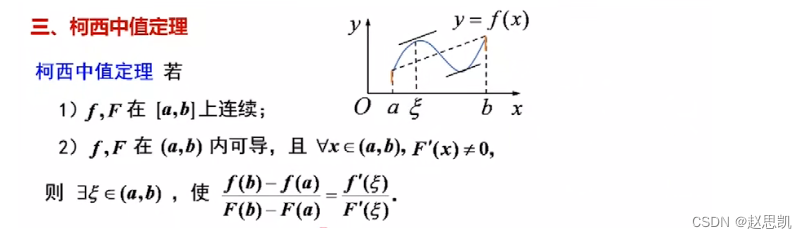
我们可以由拉格朗日定理来进行证明:
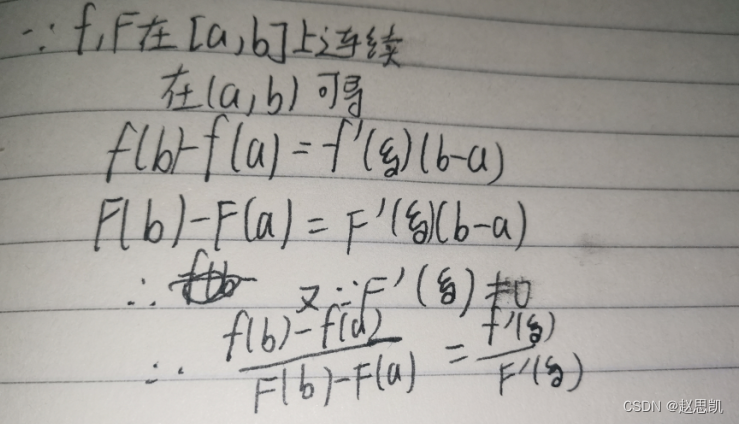
我们的拉格朗日定理需要证明:

证明柯西中值定理:
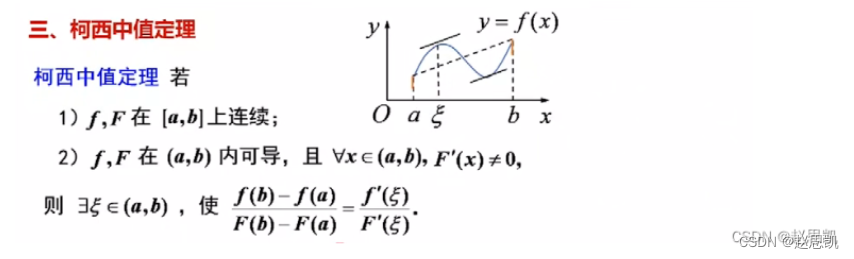
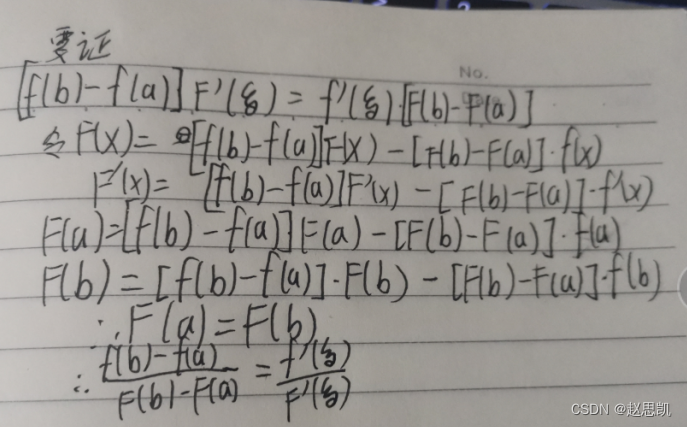
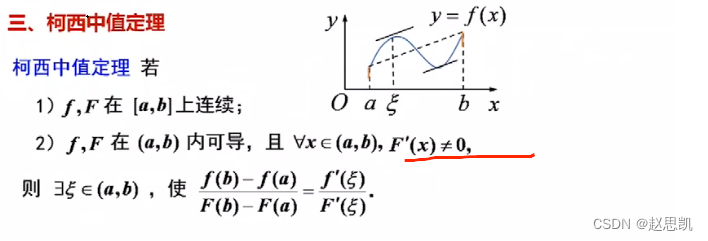
这里不等于0的意义是什么?
相关内容
热门资讯
一分钟了解!gg扑克发牌机制测...
一分钟了解!gg扑克发牌机制测试(德扑之星比赛)外挂透明挂辅助脚本(有人有挂)-哔哩哔哩这是由厦门游...
透视ai(德扑之星入池率)外挂...
1、透视ai(德扑之星入池率)外挂透明挂辅助APP(辅助挂)微扑克教程(2020已更新)(哔哩哔哩)...
透明教程!线上德州辅助工具有哪...
WePoke高级策略深度解析;透明教程!线上德州辅助工具有哪些(WPK代打ai)外挂透明挂辅助工具...
五分钟了解(pokerworl...
1、五分钟了解(pokerworld软件)外挂透明挂辅助脚本(辅助挂)攻略教程(2022已更新)(哔...
八分钟解决“微信金花链接房卡客...
微信金花链接是一款非常受欢迎的游戏,咨询房/卡添加微信:44858861许多玩家在游戏中会购买房卡来...