力扣.54,59螺旋矩阵I,II(java语言,模拟法)
题目描述:
54.螺旋矩阵:
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
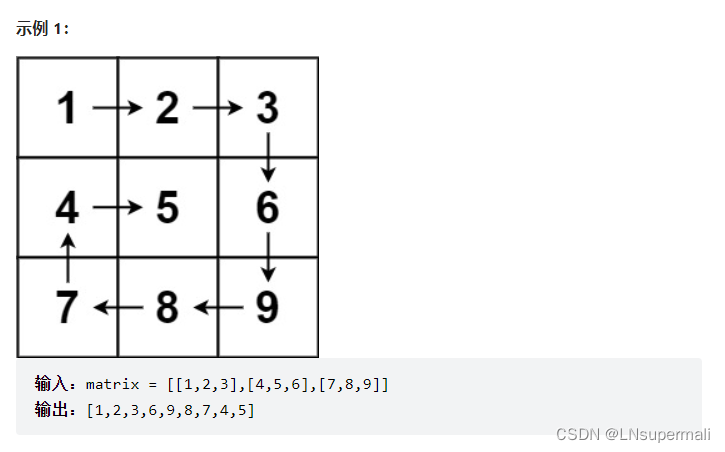

59.螺旋矩阵II
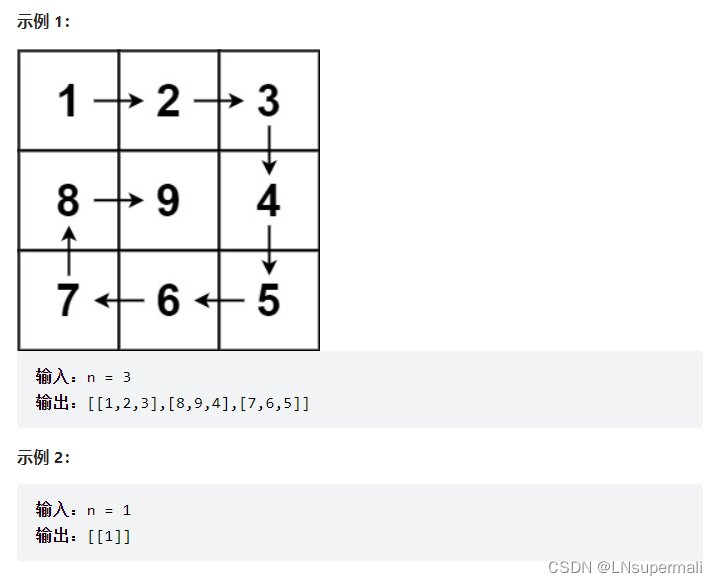
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
解题思路与代码:
54.螺旋矩阵:
对于题目所要求的"顺时针输出矩阵中的元素"我们可以使用模拟的方法来实现.我们定义四个指针left,right,top,bottom,分别初始化指向矩阵的"第一列,最后一列,第一行,最后一行",实现顺时针遍历我们即要实现从left遍历到right,从top遍历到bottom,从right遍历到left,从bottom遍历到top的循环操作但我们该注意以下几点:
1.循环退出条件为left <= right && top <= bottom:由于我们要实现的顺时针循环遍历其实是把矩阵从外向内在收缩,最后收缩到一个元素时即为left == right && top == bottom
2.从left到right后若栽从right到bottom过程中我们会发现在矩阵的右上角的元素会被遍历两次,为了避免出现重复我们就要让top++,后面的操作也要依次实现right–,bottom–,left++
代码:
class Solution { // Time Complexity: O(MN)// Space Complexity: O(N)public List spiralOrder(int[][] matrix) {//定义四个方位标记int left = 0;int right = matrix[0].length - 1;int top = 0;int bottom = matrix.length;List list = new ArrayList();while (top <= bottom && left <= right) {//从左往右for (int i = left; i <= right; i++) {list.add(matrix[top][i]);}top++;//从上到下for (int i = top; i <= bottom; i++) {list.add(matrix[i][right]);}right--;//从右到左for (int i = right; i >= left && top <= bottom; i--) {list.add(matrix[bottom][i]);}bottom--;//从下到上for (int i = bottom; i >= top && left <= right; i--) {list.add(matrix[i][left]);}left++;}return list;}
}
注意:对于从右到左,从下到上我们都要加上一个限制条件,原因就是在本代码中若不加上限制条件最后会将最后一个元素多加一次.我们举一个例子:

最后top已经大于bottom,但由于此时left == right,会使从右到左的循环再执行一次,将最后的元素6再次添加到集合中.
59.螺旋数组II
整体解法和54题一样,我们只用再定义两个变量start初始化为1,end初始化为nn,循环退出条件为start <= end*顺时针遍历时将start++依次添加入数组.
class Solution {public int[][] generateMatrix(int n) {int start = 1;int end = n * n;int left = 0;int right = n - 1;int top = 0;int bottom = n - 1;int[][] arr = new int[n][n];while (start <= end) {//从左往右for (int i = left; i <= right; i++) {arr[top][i] = start++;}top++;//从上往下for (int i = top; i <= bottom; i++) {arr[i][right] = start++;}right--;//从右往左for (int i = right; i >= left && top <= bottom; i--) {arr[bottom][i] = start++;}bottom--;//从下往上for (int i = bottom; i >= top && left <= right; i--) {arr[i][left] = start++;}left++;}return arr;}
}
上一篇:复合函数【结合例题】
