单/全源最短路的综合应用(未完待续...)
目录
- 一、单源最短路
- 1.1 AcWing 1129. 热浪
- 1.2 AcWing 1128. 信使
- 1.3 AcWing 1127. 香甜的黄油
- 1.4 AcWing 1126. 最小花费
- 1.5 AcWing 920. 最优乘车
- 1.6 AcWing 903. 昂贵的聘礼
- 1.7 AcWing 1135. 新年好
- 1.8 AcWing 340. 通信线路
一、单源最短路
1.1 AcWing 1129. 热浪
🔗 AcWing 1129. 热浪
正权图优先使用Dijkstra算法(SPFA经常被卡)。注意到题中所给图是稀疏图,因此采用邻接表的存储方式。
#include using namespace std;typedef pair PII;const int N = 2510, M = 6210 << 1; // 无向边,所以乘2int n, m, ts, te;
int h[N], e[M], ne[M], w[M], idx;
int d[N];
bool st[N];void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}void dijkstra() {memset(d, 0x3f, sizeof d);d[ts] = 0;priority_queue, greater<>> pq;pq.emplace(0, ts);while (!pq.empty()) {auto [_, t] = pq.top();pq.pop();if (st[t]) continue;st[t] = true;for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (d[j] > d[t] + w[i]) {d[j] = d[t] + w[i];pq.emplace(d[j], j);}}}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);memset(h, -1, sizeof h);cin >> n >> m >> ts >> te;while (m--) {int a, b, c;cin >> a >> b >> c;add(a, b, c), add(b, a, c); // 无向图}dijkstra();cout << d[te] << "\n";return 0;
}
1.2 AcWing 1128. 信使
🔗 AcWing 1128. 信使
因为要求的是完成整个送信过程的最短时间,所以实际上是求 max1≤i≤nd[i]\max_{1\leq i\leq n}d[i]max1≤i≤nd[i]。
#include using namespace std;typedef pair PII;const int N = 110, M = 410, INF = 0x3f3f3f3f;int n, m;
int h[N], e[M], ne[M], w[M], idx;
int d[N];
bool st[N];void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}int dijkstra() {memset(d, 0x3f, sizeof d);d[1] = 0;priority_queue, greater<>> pq;pq.emplace(0, 1);while (!pq.empty()) {auto [_, t] = pq.top();pq.pop();if (st[t]) continue;st[t] = true;for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (d[j] > d[t] + w[i]) {d[j] = d[t] + w[i];pq.emplace(d[j], j);}}}int res = 0;for (int i = 1; i <= n; i++) {if (d[i] == INF) return -1;res = max(res, d[i]);}return res;
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);memset(h, -1, sizeof h);cin >> n >> m;while (m--) {int a, b, c;cin >> a >> b >> c;add(a, b, c), add(b, a, c);}cout << dijkstra() << "\n";return 0;
}
1.3 AcWing 1127. 香甜的黄油
🔗 AcWing 1127. 香甜的黄油
首先注意到 P3P^3P3 可达 5×1085\times 10^85×108,因此使用Floyd算法基本会TLE,所以此题只能采用单源最短路算法。
思路是以每个点为起点进行一次最短路算法,不断更新最小值。
Dijkstra实现:
#include using namespace std;typedef pair PII;const int N = 810, M = 2910, INF = 0x3f3f3f3f;int k, n, m;
int h[N], e[M], ne[M], w[M], idx;
int d[N], cnt[N]; // cnt[i]代表牧场i有多少头奶牛
bool st[N];void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}int dijkstra(int s) {memset(st, 0, sizeof st); // 因为dijkstra会被多次调用,所以每次都需要初始化memset(d, 0x3f, sizeof d);d[s] = 0;priority_queue, greater<>> pq;pq.emplace(0, s);while (!pq.empty()) {auto [_, t] = pq.top();pq.pop();if (st[t]) continue;st[t] = true;for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (d[j] > d[t] + w[i]) {d[j] = d[t] + w[i];pq.emplace(d[j], j);}}}int res = 0;for (int i = 1; i <= n; i++) {if (cnt[i] && d[i] == INF) return INF; // 当牧场i有牛时且从起点s不可抵达牧场i,说明s必不可能是我们需要的那个牧场res += d[i] * cnt[i];}return res;
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);memset(h, -1, sizeof h);cin >> k >> n >> m;while (k--) {int t;cin >> t;cnt[t]++;}while (m--) {int a, b, c;cin >> a >> b >> c;add(a, b, c), add(b, a, c);}int ans = INF;for (int i = 1; i <= n; i++) // 以每个点为起点进行一次dijkstraans = min(ans, dijkstra(i));cout << ans << "\n";return 0;
}
时间复杂度为 O(nmlogn)O(nm\log n)O(nmlogn)。
SPFA实现:
#include using namespace std;const int N = 810, M = 2910, INF = 0x3f3f3f3f;int k, n, m;
int h[N], e[M], ne[M], w[M], idx;
int d[N], cnt[N]; // cnt[i]代表牧场i有多少头奶牛
bool st[N];void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}int spfa(int s) {memset(st, 0, sizeof st);memset(d, 0x3f, sizeof d);d[s] = 0;queue q;q.push(s);st[s] = true;while (!q.empty()) {auto t = q.front();q.pop();st[t] = false;for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (d[j] > d[t] + w[i]) {d[j] = d[t] + w[i];if (!st[j]) {q.push(j);st[j] = true;}}}}int res = 0;for (int i = 1; i <= n; i++) {if (cnt[i] && d[i] == INF) return INF;res += d[i] * cnt[i];}return res;
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);memset(h, -1, sizeof h);cin >> k >> n >> m;while (k--) {int t;cin >> t;cnt[t]++;}while (m--) {int a, b, c;cin >> a >> b >> c;add(a, b, c), add(b, a, c);}int ans = INF;for (int i = 1; i <= n; i++) // 以每个点为起点进行一次spfaans = min(ans, spfa(i));cout << ans << "\n";return 0;
}
时间复杂度为 O(nm)O(nm)O(nm)(如果不卡的话)。
此题使用SPFA大约380ms,使用Dijkstra大约2300ms。
1.4 AcWing 1126. 最小花费
🔗 AcWing 1126. 最小花费
设 AAA 有 xxx 元,每次转账需要扣除 zi%z_i\%zi% 的手续费,假设共转账 nnn 次,容易得到
x=100⋅∏i=1n11−0.01⋅zix=100\cdot \prod_{i=1}^n\frac{1}{1-0.01\cdot z_i} x=100⋅i=1∏n1−0.01⋅zi1
要最小化 xxx,我们可以以 BBB 为起点执行Dijkstra算法,初始时令 d[b] = 100,最后 d[a] 就是我们所需的答案。
#include using namespace std;typedef pair PDI; // 注意距离是浮点数const int N = 2010, M = 2e5 + 10, INF = 0x3f3f3f3f; // 注意M必须开两倍int n, m, a, b;
int h[N], e[M], ne[M], w[M], idx;
double d[N]; // 注意类型
bool st[N];void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}void dijkstra() {for (int i = 1; i <= n; i++) d[i] = INF; // 因为d是浮点型数组,所以用for循环初始化d[b] = 100;priority_queue, greater<>> pq;pq.emplace(100, b);while (!pq.empty()) {auto [_, t] = pq.top();pq.pop();if (st[t]) continue;st[t] = true;for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (d[j] > d[t] / (1 - 0.01 * w[i])) {d[j] = d[t] / (1 - 0.01 * w[i]);pq.emplace(d[j], j);}}}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);memset(h, -1, sizeof h);cin >> n >> m;while (m--) {int x, y, z;cin >> x >> y >> z;add(x, y, z), add(y, x, z);}cin >> a >> b;dijkstra();cout << fixed << setprecision(8) << d[a] << "\n";return 0;
}
1.5 AcWing 920. 最优乘车
🔗 AcWing 920. 最优乘车
本题的主要难点是数据的读取和建图方式。
先看下面的例子。
💡 第一行是一个整数 mmm,表示接下来将有 mmm 行由空格隔开的整数,且每行的整数个数未知,请问该如何读取?
int m;
cin >> m;string line;
getline(cin, line); // 由于getline会读取到换行符,因此我们需要先把m后面的换行符读掉
while (m--) {getline(cin, line);stringstream ssin(line);int x;while (ssin >> x) {// 其他操作}
}
⚠️ 注意,也可以使用
getchar()来过滤掉 mmm 后面的换行符,但在关闭了同步流的情况下混用getchar()和getline()会出现意想不到的错误。
接下来考虑如何建图。由于无法事先预估出具体的边数,并且图中的节点数也较少,因此可以用邻接矩阵来存图。一个问题是,我们要求的不是最短路而是最少换乘次数,例如,假设只有一条巴士线路 1 -> 2 -> 3 -> 4,从 1 到 4 的最短路长度为 333,而换乘次数为 000。
为解决这一问题,我们可以对于巴士线路的每个节点都向它的后继节点连一条有向边,即
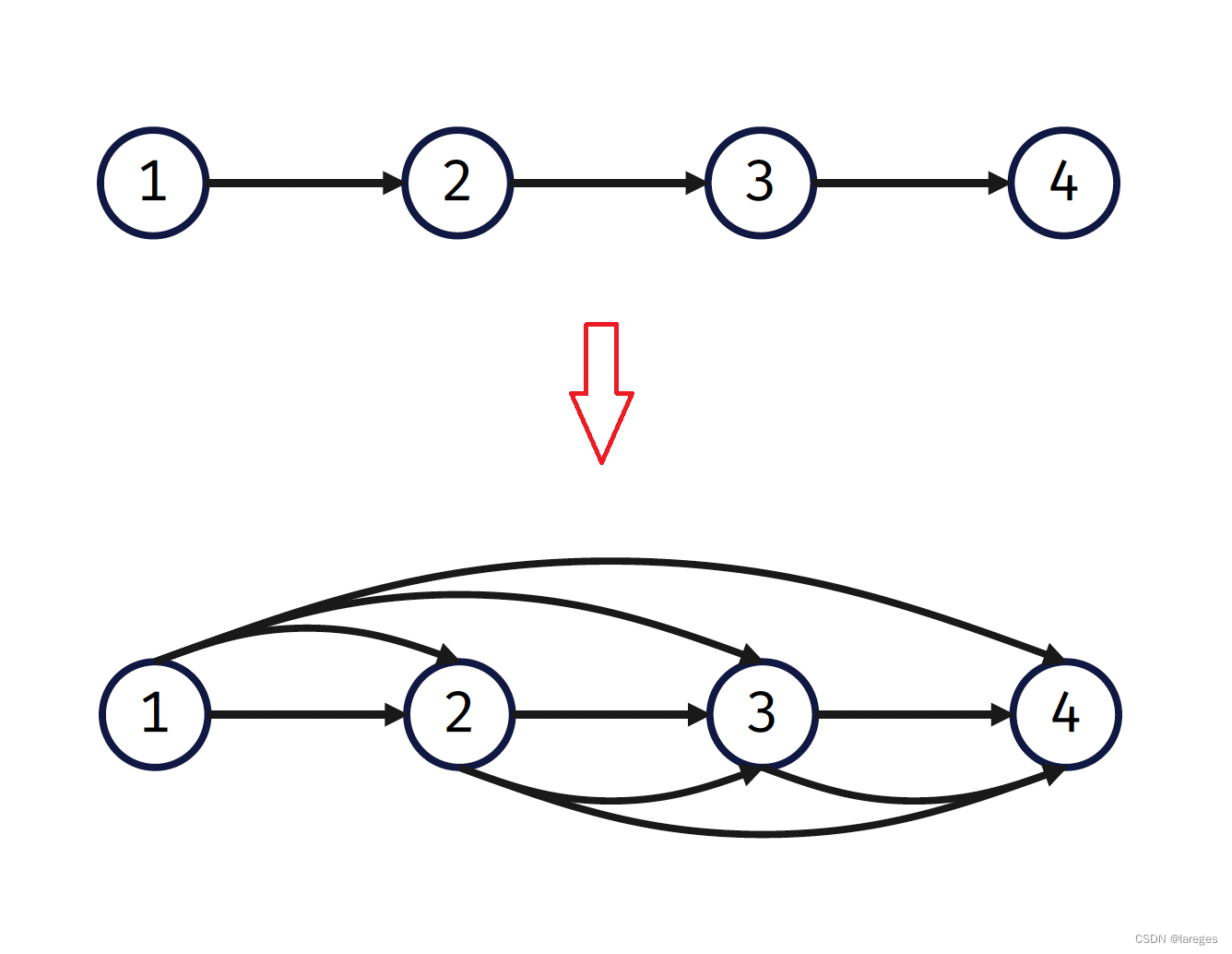
从而换乘次数就是最短路长度减 111。由于边权都相同,因此可以求最短路长度可以直接使用BFS。
#include using namespace std;const int N = 510, INF = 0x3f3f3f3f;int m, n;
int g[N][N];
int d[N];
bool st[N];void bfs() {memset(d, 0x3f, sizeof d);d[1] = 0;queue q;q.push(1);st[1] = true;while (!q.empty()) {auto t = q.front();q.pop();for (int j = 1; j <= n; j++) {if (g[t][j] && !st[j]) {q.push(j);d[j] = d[t] + 1;st[j] = true;}}}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cin >> m >> n;string line;getline(cin, line); // 去掉第一行最后的换行符while (m--) {getline(cin, line);stringstream ssin(line);vector row; // 存储一条巴士线路int x;while (ssin >> x) row.push_back(x);for (int i = 0; i < row.size() - 1; i++)for (int j = i + 1; j < row.size(); j++)g[row[i]][row[j]] = 1;}bfs();if (d[n] == INF) cout << "NO\n";else cout << max(d[n] - 1, 0) << "\n"; // 当起点和终点重合时,换乘次数为-1,而实际应当是0return 0;
}
1.6 AcWing 903. 昂贵的聘礼
🔗 AcWing 903. 昂贵的聘礼
先不考虑等级限制,我们来看如何建图。
如果物品 iii 有替代品 jjj,那我们就画一条从 jjj 到 iii 的有向边 j→wij\xrightarrow{w}ijwi,其中 www 代表使用替代品 jjj 后物品 iii 的优惠价格。
以题中所给数据为例,我们可以得到如下的有向图:
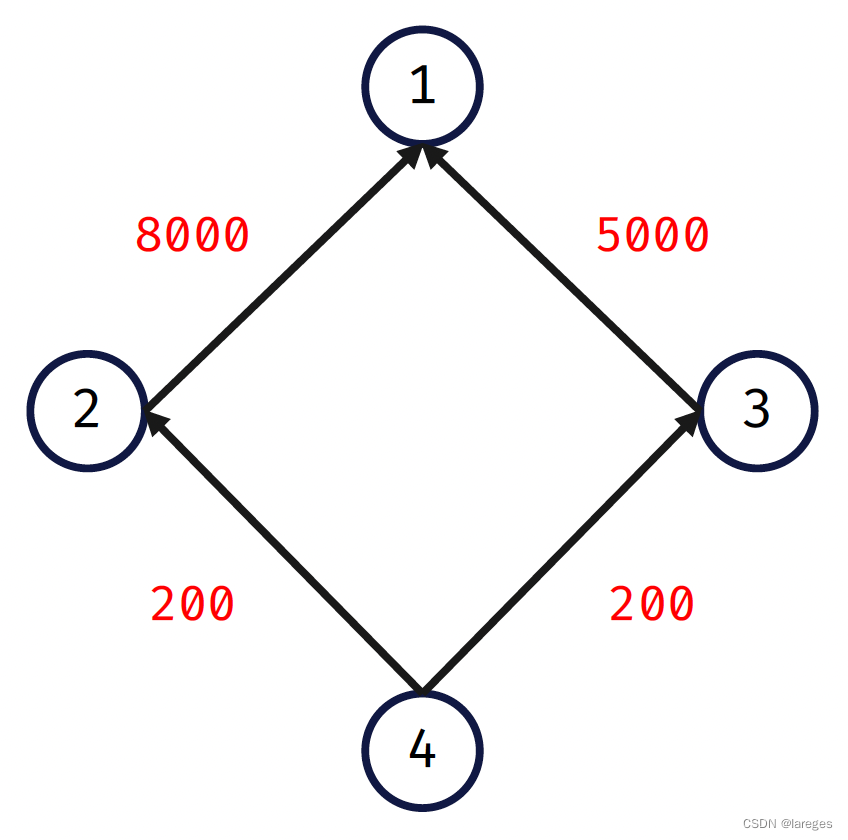
我们从 444 出发,即先购买物品 444,然后沿着 4 -> 3 -> 1 的路径行进到终点 111,此时花费的总金币最少,为 50+200+5000=525050+200+5000=525050+200+5000=5250。
但这并不是我们所熟知的最短路,因为除了边权之外,我们还加上了出发点本身的价格(因为我们至少要先购买一个物品才能不断去替代)。为解决这一问题,我们可以建立一个超级源点 000,并让 000 指向图中所有的节点,其中 0→wi(i=1,2,3,4)0\xrightarrow{w}i\,(i=1,2,3,4)0wi(i=1,2,3,4) 中的 www 代表物品 iii 本身的价格,如下图所示:
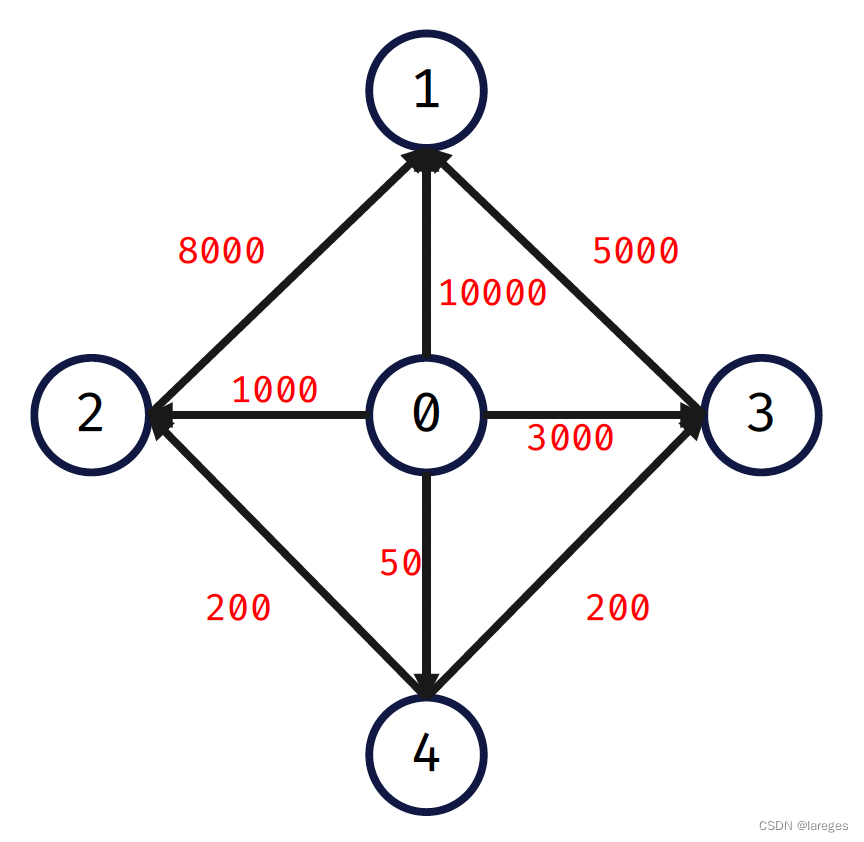
于是问题归结成寻找以 000 为起点,111 为终点的最短路。
现在考虑等级限制,由于最终必须要购买物品 111,不妨设物品 111 的主人(酋长)的地位等级为 l1l_1l1,于是对于最短路上的某一节点 iii,必须有 ∣l1−li∣≤m|l_1-l_i|\leq m∣l1−li∣≤m(题目中没有明确说明酋长的地位等级是最高的,因此这里必须使用绝对值),否则最终无法与酋长进行交易,展开可得
li∈[l1−m,l1+m],i=2,3,⋯,nl_i\in[l_1-m,\,l_1+m],\quad i = 2,3,\cdots,n li∈[l1−m,l1+m],i=2,3,⋯,n
除此之外还需满足
∣li−lj∣≤m,i,j∈{2,3,⋯,n}|l_i-l_j|\leq m,\quad i,j\in\{2,3,\cdots,n\} ∣li−lj∣≤m,i,j∈{2,3,⋯,n}
于是我们只需在区间 [l1−m,l1+m][l_1-m,\,l_1+m][l1−m,l1+m] 中枚举长度为 mmm 的区间并不断更新最小值。
#include using namespace std;typedef pair PII;const int N = 110, M = 10110, INF = 0x3f3f3f3f;int m, n;
int h[N], e[M], ne[M], w[M], idx;
int d[N], level[N]; // level[i]代表第i个物品的主人的地位等级
bool st[N];void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}int dijkstra(int l, int r) {memset(st, 0, sizeof st); // 因为dijkstra会被多次调用memset(d, 0x3f, sizeof d);d[0] = 0; // 起点是0号点,终点是1号点priority_queue, greater<>> pq;pq.emplace(0, 0);while (!pq.empty()) {auto [_, t] = pq.top();pq.pop();if (st[t]) continue;st[t] = true;for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (d[j] > d[t] + w[i] && level[j] >= l && level[j] <= r) {d[j] = d[t] + w[i];pq.emplace(d[j], j);}}}return d[1];
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);memset(h, -1, sizeof h);cin >> m >> n;for (int i = 1; i <= n; i++) {int p, x;cin >> p >> level[i] >> x;add(0, i, p); // 建立超级源点到每个物品之间的连接while (x--) {int t, v;cin >> t >> v;add(t, i, v); // 建立替代品到该物品之间的连接}}int ans = INF;for (int i = level[1] - m; i <= level[1]; i++)ans = min(ans, dijkstra(i, i + m)); // 枚举所有长度为m的区间cout << ans << "\n";return 0;
}
1.7 AcWing 1135. 新年好
🔗 AcWing 1135. 新年好
首先需要注意,本题并不是求 max(d[a], d[b], d[c], d[d], d[e]),因为这样并不能保证最短路上同时含有 a, b, c, d, e 这五个点。
由于题目允许以任意的顺序去拜访亲戚,所以我们可以暴力枚举出每一种顺序,共有 5!=1205!=1205!=120 种。对于每种顺序,我们都需要跑 555 次Dijkstra来求出拜访完所有亲戚的总时间。例如,对于顺序 1 -> a -> b -> c -> d -> e,我们需要先以 1 为起点跑一次Dijkstra求出 1 到 a 的最短路,再以 a 为起点跑一次Dijkstra求出 a 到 b 的最短路,依次类推。总计算量为 120⋅5⋅mlogn≈600⋅105⋅15=9⋅108120\cdot 5\cdot m\log n\approx600\cdot 10^5\cdot 15=9\cdot 10^8120⋅5⋅mlogn≈600⋅105⋅15=9⋅108,显然会TLE。
事实上,我们可以反过来做,即先跑 666 次Dijkstra预处理出 1,a,b,c,d,e1,a,b,c,d,e1,a,b,c,d,e 这六个点到其他所有点的最短路,然后再枚举所有的拜访顺序,这样一来,总计算量为 6⋅mlogn+5!≈6⋅105⋅15+120≈9⋅1066\cdot m\log n+5!\approx6\cdot 10^5\cdot15+120\approx9\cdot 10^66⋅mlogn+5!≈6⋅105⋅15+120≈9⋅106。
我们可以开一个二维数组 dist[6][N] 来保存六个点到其他所有点的最短路。其中 dist[0][N] 存储 111(起点)到其他所有点的最短路,dist[1][N] 存储 aaa 到其他所有点的最短路,dist[2][N] 存储 bbb 到其他所有点的最短路,以此类推。
#include using namespace std;typedef pair PII;const int N = 50010, M = 2e5 + 10, INF = 0x3f3f3f3f;int n, m;
int h[N], e[M], ne[M], w[M], idx;
int dist[6][N], source[6];
bool st[N];void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}void dijkstra(int s, int d[]) {memset(st, 0, sizeof st);memset(d, 0x3f, N * 4); // 此处不可以使用sizeof dd[s] = 0;priority_queue, greater<>> pq;pq.emplace(0, s);while (!pq.empty()) {auto [_, t] = pq.top();pq.pop();if (st[t]) continue;st[t] = true;for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (d[j] > d[t] + w[i]) {d[j] = d[t] + w[i];pq.emplace(d[j], j);}}}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);memset(h, -1, sizeof h);cin >> n >> m;source[0] = 1;for (int i = 1; i < 6; i++) cin >> source[i];while (m--) {int x, y, z;cin >> x >> y >> z;add(x, y, z), add(y, x, z);}for (int i = 0; i < 6; i++) dijkstra(source[i], dist[i]);vector indices(6);iota(indices.begin(), indices.end(), 0);int ans = INF;do {int res = 0;for (int i = 0; i < 5; i++) res += dist[indices[i]][source[indices[i + 1]]];ans = min(ans, res);} while (next_permutation(indices.begin() + 1, indices.end()));cout << ans << "\n";return 0;
}
1.8 AcWing 340. 通信线路
🔗 AcWing 340. 通信线路
分析题意不难发现,我们需要找到从 111 到 nnn 的一条路径,于是农场主的花费就是第 k+1k+1k+1 大的边权。
但问题是,从 111 到 nnn 可能不止一条路径,因此实际上求的是所有第 k+1k+1k+1 大边权的最小值。此外,如果某条路径的边数小于等于 kkk,那么农场主的花费为 000。当然,111 和 nnn 之间也可能不存在路径。
我们可以采用二分的方法,即对区间 [0,106+1][0, 10^6+1][0,106+1] 二分。
#include using namespace std;typedef pair PII;const int N = 1010, M = 20010, INF = 0x3f3f3f3f;int n, m, k;
int h[N], e[M], ne[M], w[M], idx;
int d[N];
bool st[N];void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}bool check(int x) {memset(st, 0, sizeof st);memset(d, 0x3f, sizeof d);d[1] = 0;priority_queue, greater<>> pq;pq.emplace(0, 1);while (!pq.empty()) {auto [_, t] = pq.top();pq.pop();if (st[t]) continue;st[t] = true;for (int i = h[t]; ~i; i = ne[i]) {int j = e[i], W = w[i] > x;if (d[j] > d[t] + W) {d[j] = d[t] + W;pq.emplace(d[j], j);}}}return d[n] <= k;
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);memset(h, -1, sizeof h);cin >> n >> m >> k;while (m--) {int x, y, z;cin >> x >> y >> z;add(x, y, z), add(y, x, z);}int l = 0, r = 1e6 + 1;while (l < r) {int mid = l + r >> 1;if (check(mid)) r = mid;else l = mid + 1;}if (r == 1e6 + 1) r = -1;cout << r << "\n";return 0;
}
