🎆音乐分享（点击链接可以听哦）

 夏天的风_蓝心羽
 

---

 

目录

⭐什么是dfs

✨排列型枚举（全排列）

✨排列型枚举（全排列变形） 

✨组合型枚举

✨指数型枚举 

✨dfs的应用 

⭐什么是dfs

就是深度优先遍历，顾名思义，就是沿着一条路一直走到头，然后再回头 

 具体方法请看下面的题目

 🚥🚥🚥🚥🚥🚥

排列型枚举（全排列）

94. 递归实现排列型枚举 - AcWing题库

把 1∼n 这 n 个整数排成一行后随机打乱顺序，输出所有可能的次序。

输入格式

一个整数 n。

输出格式

按照从小到大的顺序输出所有方案，每行 1 个。

首先，同一行相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面。

 

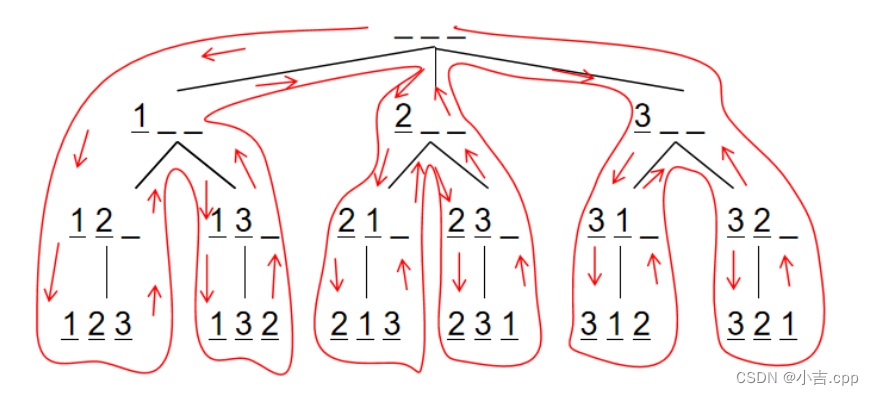
 从一条路遍历到头后，然后再回溯

#include
using namespace std;
const int N=100100;
int a[N],b[N];
int n,m;
void dfs(int x)
{if(x==m+1){for(int i=1;i<=m;i++){printf("%d ",a[i]);}return;}for(int i=1;i<=m;i++){if(b[i]==0){a[x]=i;//这里是xb[i]=1;dfs(x+1);b[i]=0;}}return;
}
int main()
{cin>>m;dfs(1);
}

🚕🚕🚕🚕🚕🚕 

排列型枚举（全排列变形） 

1537. 递归实现排列类型枚举 II - AcWing题库 

#include 
#include using namespace std;const int N = 10;int n;
int a[N], nums[N];         
bool st[N];void dfs(int u)
{if (u == n){for (int i = 0; i < n; i ++ ) cout << nums[i] << ' ';cout << endl;return;}for (int i = 0; i < n; i ++ )if (!st[i]){nums[u] = a[i];st[i] = true;dfs(u + 1);         st[i] = false;      //还原现场while (i + 1 < n && a[i + 1] == a[i]) i ++ ;        //跳过重复的}
}int main()
{cin >> n;for (int i = 0; i < n; i ++ ) cin >> a[i];sort(a, a + n);     //排序后重复的数字就会排在一起，便于去重dfs(0);return 0;
}

 🚕🚕🚕🚕🚕🚕

组合型枚举

93. 递归实现组合型枚举 - AcWing题库 

从 1∼n 这 n 个整数中随机选出 m 个，输出所有可能的选择方案。

输入格式

两个整数 n,m ,在同一行用空格隔开。

输出格式

按照从小到大的顺序输出所有方案，每行 1 个。

首先，同一行内的数升序排列，相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面

（例如 1 3 5 7 排在 1 3 6 8 前面）。

 

 

 

#include 
using namespace std;
int n,m;
const int N=100010;
int a[N],b[N];
void dfs(int x, int start)
{if(x+n-start < m)return;if(x == m+1){for(int i = 1; i <= m; i++)printf("%d ", a[i]);puts("");return;}for(int i = start; i <= n; i++)// i从start开始  i<= n{if(b[i]==0){a[x]=i;//是xb[i]=1;dfs(x+1, i+1);b[i]=0;}}return;
}int main()
{scanf("%d%d", &n, &m);dfs(1, 1);return 0;
}

🚕🚕🚕🚕🚕🚕 

指数型枚举 

92. 递归实现指数型枚举 - AcWing题库

 

题目描述
从 1~n 这 n 个整数中随机选取任意多个，输出所有可能的选择方案。

输入格式
输入一个整数n。

输出格式
每行输出一种方案。

同一行内的数必须升序排列，相邻两个数用恰好1个空格隔开。

对于没有选任何数的方案，输出空行。

本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

#include 
using namespace std;
typedef long long ll;int n;
int a[20];
bool vis[20];// 一共tar个坑，当前枚举到第pos个坑
void dfs(int pos, int tar) {if (pos == tar + 1) {for (int i = 1; i <= tar; i ++ ) cout << a[i] << " ";cout << endl;return ;}// 选数填坑for (int i = 1; i <= n; i ++) {if (!vis[i]) {vis[i] = true; a[pos] = i;dfs (pos + 1, tar);vis[i] = false;}}
}int main() {cout << endl; // 不取cin >> n;for (int i = 1; i <= n; i ++ )//主要是这一步，控制了每次取的数字个数不同dfs(1, i);return 0;
}

 🚕🚕🚕🚕🚕🚕

dfs的应用 

4868. 数字替换 - AcWing题库 

给定两个整数 n,x。

你可以对 x 进行任意次以下操作：

• 选择 x 的一位数字 y，将 x 替换为 x*y。

请你计算通过使用上述操作，将 x变为一个 n 位数字（不含前导 0），所需要的最少操作次数。

例如，当 n=3,x=2时，对 2 进行如下 4 次操作，即可使其变为 3 位数字：

1. 将 2 替换为 2×2=4。
2. 将 4 替换为 4×4=16。
3. 将 16 替换为 16×6=96。
4. 将 96 替换为 96×9=864。

输入格式

共一行，包含两个整数 n,x。

输出格式

一个整数，表示将 x 变为一个 n 位数字，所需要的最少操作次数。

如果无解，则输出 -1。

 

 

#include 
#include 
#include using namespace std;typedef long long LL;const int INF = 1000;int n;
int ans = INF;void dfs(LL x, int d)
{bool st[10] = {0};int cnt = 0;for (LL y = x; y; y /= 10){cnt ++ ;st[y % 10] = true;//把不同位数分开}if (d + n - cnt >= ans) return;//如果当前位数+结果要求的位数-当前的位数>=结果，不成立，结束运行if (cnt == n){ans = d;return;}for (int i = 9; i >= 2; i -- )if (st[i])//如果存在这个位数dfs(x * i, d + 1);
}int main()
{LL x;cin >> n >> x;dfs(x, 0);if (ans == INF) ans = -1;cout << ans << endl;return 0;
}

🚕🚕🚕🚕🚕🚕

Code over!